What’s new?
Today’s announcement was 1542 new local cases in NSW is consistent with the observation that growth of cases has slowed, and that we may be approaching, or have reached, the peak number of new cases. This is a hopeful sign. The cumulative case projection for today from 7 days ago is overestimating by 6% of the actual value.
Despite the uncertainty inherent in the model, that a peak was arriving has been suggested by the Richards’ growth curve model for at least the past fortnight (see below).
It is possible that the apparent peak is some sort of artifact in the reporting of cases (e.g., a delay in processing specimens). If this is the case, it should be very obvious in the coming couple of the days with a seeming explosion in the new case counts, with cases following the Gompertz model projections (as seen on the “4 plot” chart). My view is that this seems to be the less probable of explanations, especially with data from the course of this week.
The flexible nature of the Richards’ growth curve model at this point means that there is some significant uncertainty regarding the trajectory of the growth in the near future. Any estimates, even in the immediate days needs to be taken cautiously. Simply, a rapid fall in the number of cases as suggested by the model estimates is not especially plausible. Most likely, the model will self correct as more data from the coming days become available. The model suggests that we are likely to see around 5000-7500 new cases over the next 7 days. The caveat here is that a higher rather than lower part of the estimate is more probable, and indeed, it may simply be a substantial underestimate.
I’ve changed the way I estimate the new daily cases from the model along with how I compute the 95% confidence intervals. I’m not likely to change this again as I’m finally happy with the statistical reasoning underlying the process. In essence, I use the standard errors of the parameters of the model fitted through non-linear regression (the Richards’ growth curve model has 5 parameters, while the Gompertz model has 4 parameters) to create a distribution of values for these parameters. Using these, I then bootstrap an estimate of the daily new cases along with a distribution of these cases through simulation. As per the comments section in the code:
# I've changed the way I compute the 95% confidence intervals on several occasions. # Initially, I couldn't think of how to easily compute this, so I resorted to a hack. # I basically used the confidence interval of the estimate from the model of the # cumulative cases as the estimate for the CI of the derivative. This would obviously # be an overestimate. # # On 7 August 2021, I changed the method to be more statistically defensible. # For each day's TOTAL case number projection in the fitted Gompertz/Richards' model, I use # the standard error of that fitted value to create a randomised normal distribution of # values. I compute a list of 1,000,000 values for each day. I then subtract a list of # these values from the list of the prior day, effectively creating a list of differences # between the days. This distribution of values will be overly conservative as in reality # it is not possible for the total number of cases to ever be less than a previous day's. # # On 9 September 2021, I changed the method once again, which I think is finally acceptable. # Both the Gompertz and Richards' models give standard errors for each of the parameters. # I use this to create a randomised normal distribution of these parameters, and then use # these parameters to simulate new curves in a bootstrapping process (a run of 10,000 times). # From each of these simulated growth curves, I extract the daily growth in new cases. For # each day, the median, or middle value of this list of differences is the NEW case estimate # as directly computed from the model. Specific percentiles, which are the proportion of # values of the distribution can be interpreted as the confidence interval. For instance, the # 95% confidence interval is the interval between the 2.5% and 97.5% centiles.
Context and timeline of the Sydney 2021 outbreak
I started these analysis in early July with the new COVID-19 (delta variant) outbreak in Sydney NSW. The purpose of these charts is that they provide some projections into the near future. Hopefully this allows for some data driven expectations. The Sydney 2021 series starts on 12 July 2021 and are available here: https://vitualis.com/?page_id=4071
The current Sydney outbreak started on 17 June 2021 – the first day with reports of community cases in Bondi. The NSW Government formally commenced stay-at-home orders (“lockdown”) for a number of inner-Sydney regions on 25 June 2021 at 2359, having announced this earlier in the day. This was then broadened 18 hours later to cover the whole of Greater Sydney. The initial plan was a two-week lockdown, with it potentially being lifted on 9 July 2021.
By 9 July 2021, there were early signs that COVID-19 transmission was worsening. On 15 July 2021, the lockdown was again extended until the end of July, and then extended again, this time for four weeks on 28 July 2021. Conditions at the end of the month for people living with South Western, and Western Sydney included a limit to travelling only 5 km from home, masks at all times outside, with only essential workers allowed to leave the local government area, with the requirement of a COVID-19 swab every 72 hours.
On 14 August 2021, in the setting of rapidly rising case counts, further restrictions were announced. The 5 km radius limit (from 10 km) was extended to all residents in Greater Sydney, starting 16 August 2021. Permits were also now required to leave the Greater Sydney area. Furthermore, stay-at-home orders were extended to across the entire state of NSW.
On 20 August 2021, the lockdown in Greater Sydney was extended to the end of September, and a range of new restrictions stated on 23 August 2021 in the “hot” LGAs including an overnight curfew, restricting outdoor exercise to an hour a day, closure of most businesses except for click-and-collect, and increased policing powers.
Projection of new daily cases, and cumulative counts of COVID-19 with data up to 10 September 2021
What is this?
The top image is a chart of the cumulative (total) COVID-19 cases in NSW, starting from 17 June 2021, and the lower image is a chart of the daily new cases. Only local cases are included (i.e., excluding cases identified in quarantine). Projections are given for the next 7 days. It should be noted that estimates have high levels of uncertainty beyond a few days and must be interpreted cautiously.
The projections are made using a model by fitting the cumulative case data since 17 June 2021 to a Richards’ growth curve using non-linear regression. The dark central dashed lines are the model estimates, with 95% confidence intervals of the estimate. On the lower chart, the colour gradations can be understood as the degree of uncertainty in the model projections.
Gompertz and Richards’ growth curve
The Gompertz function is a type of sigmoid, or “S”-shaped curve. It’s been around since the early 19th century and was initially used to describe and model demographic mortality curves, and hence, well known to actuaries. The Gompertz function can also be used to accurately model biological growth (e.g., epidemics, tumour size, enzymatic reactions). I have chosen to use this model to help with creating insights as earlier in the pandemic, it was found to be useful in modelling cumulative cases of COVID-19 from the Chinese outbreaks (Jia et al. arXiv:2003.05447v2 [q-bio.PE]).
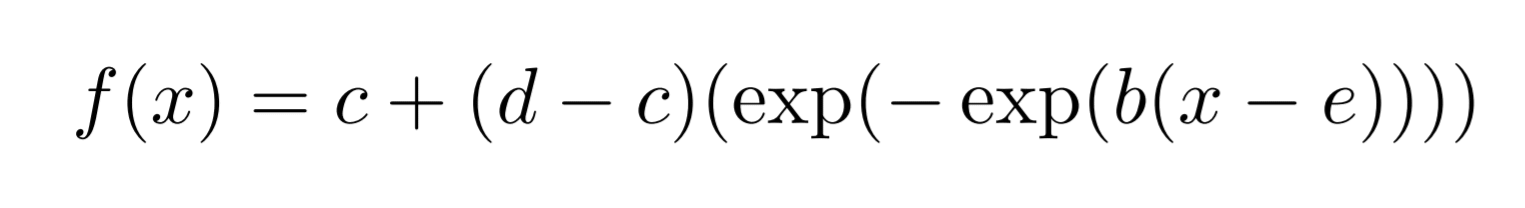
The Richards’ growth curve (or the generalised logistic function), which is a broad family of sigmoid (S-shaped) curves that can describe well many types of growth, including epidemics. It has also been demonstrated to have utility in modelling COVID-19 outbreaks in 2020 (Lee et al. PLoS One 2020 doi: 10.1371/journal.pone.0236860).
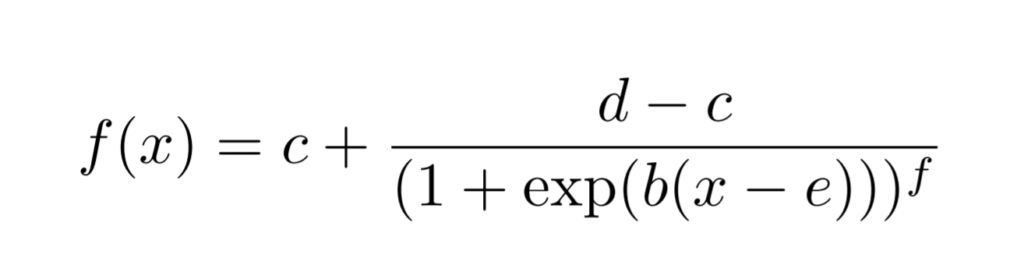
I’m using the parameterisation of these functions through the drc package: https://cran.r-project.org/web/packages/drc/drc.pdf
Why the changes?
I’ve undertaken some assessment of the degree of predictive error in both the Gompertz and Richards’ growth curve models. These charts compare the 7- and 14-day total case projections of the models, to what actually occurred in reality 7 and 14 days later. For interpretation, above the 0% error line means that the model provided an over-estimate compared to reality, and below the 0% error line an underestimate.
Both models were in early July providing substantial underestimates, which is what I suspected when I started this series. The Richards’ growth curve model has struggled with the fit to the data, with poor predictive accuracy in July. Both models have been gradually underestimating further since the beginning of August. By mid-late August, the Richards’ growth curve model was clearly outperforming the Gompertz model. By early September, the Gompertz model had self-corrected.
The Richards’ growth curve model – today vs projections from 7- and 14-days ago
I don’t publish the future projections beyond 7 days as these are uncertain and I’m concerned about the risk of misleading members of the public. The further one goes into the future, the more likely that the assumptions of the model are a poor fit and description for reality. On this occasion, I’m going to retrospectively compare the projections from 7- and 14-days ago to the projection from today, with axes at the same scale. The data points including today are included in all the charts, but the projections from 7- and 14-days ago only use the data up to that date. The Richards’ growth curve model has actually been quite stable over the last fortnight, including the identification of a peak arriving in September.
The overall the trend we can see is as the time progresses with more data, the confidence intervals narrow. The peak of the hump in the last week moved earlier, also resulting in a lower height. This is on the assumption that we are at the peak at all. If the Gompertz model is correct, it effectively gives a dissenting and incompatible projection that cases will continue to rise.
Daily case trends
Comparison between the Gompertz and Richards’ growth curve model projections, along with smoothed data trends (7-day simple moving average, and GAM) with data up to 10 September 2021
The generalised additive model gives a descriptive “reality check” to the models. The GAM can be considered as an advanced smoothed trend of the daily counts. At present, there is notable incompatibility between the Gompertz and Richards’ growth curve models.
Want to know more?
Primary data source is from NSW Health for daily new cases. The analysis is performed using RStudio Cloud using R version 4.1.0.
